quarta-feira, 26 de fevereiro de 2014

ondas modulares Graceli visa a amplitude de variações de formas, Ângulos, e variações em relação a sistema quadrimensional Graceli, infinitésimos sequenciais, e em relação de variações em relação ao tempo e movimentos, espaços, variações sequenciais matemáticas e ao tempo..





A forma padrão de uma onda modulada em amplitude (AM) é definida como:
s(t)=A_{c}[1+k_{a}m(t)]cos(2\pi f_{c}t) +  = f + ày+àn.... + Llam logx/x n... [*R, 0 –R [A] logx/x....+ â [grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx + rot, + transl. + acel /t /c/t.







e(t)=(E_{c}+e_{m}(t))\cos(2\pi f_{c}t) +  = f + ày+àn.... + Llam logx/x n... [*R, 0 –R [A] logx/x....+ â [grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx + rot, + transl. + acel 
/t /c/t
 .




Onde:
E_{c}=Amplitude da portadora (c subscrito é de carrier- portadora)
e_{m}(t)=Função do sinal modulador (m subscrito de modulador)
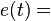e(t)=Função da onda modulada
f_{c}=Frequência da portadora
Como pode ser visto nesta função, a portadora é uma função cossenoidal simples com frequência fc e cuja amplitude varia de em torno de uma amplitude base Ec, de acordo com uma função de um sinal modulador em(t).
Sabe-se, que toda e qualquer função pode ser descrita como uma soma (finita ou infinita) de senoides e cossenoides. Desta forma, a função da onda moduladora pode ser descrita como uma soma de cossenoides. Vamos analisar aqui o que acontecerá se e_{m}(t) for uma função cosseno simples com frequência do modulador fm:






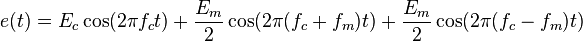e(t)=E_{c}\cos(2\pi f_{c}t)+{\frac {E_{m}}{2}}\cos(2\pi (f_{c}+f_{m})t)+{\frac {E_{m}}{2}}\cos(2\pi (f_{c}-f_{m})t) +   f + ày+àn.... + Llam logx/x n... [*R, 0 –R [A] logx/x....+ â [grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx + rot, + transl. + acel 
/t /c/t
 .





Na demodulação, basta aplicar o mesmo procedimento utilizado para a modulação. Entretanto, é aqui que reside um ponto negativo do DSB-SC: para a demodulação ocorrer correctamente, é necessário que exista um sincronismo entre a portadora utilizada na modulação e a utilizada na demodulação, caso contrário o sinal não será correctamente demodulado. A solução para este problema será visto adiante, no método de modulação em amplitude que é empregado nas transmissões de rádios comerciais AM.
O sinal transmitido é então novamente multiplicado pela mesma senóide utilizada como portadora. Assim, obtém-se:


para um sistema de frequência variável pelo tempo, movimentos, e sistema de ondas variaveis temos:
x(t)\cos ^{2}{\omega }{t}\Longleftrightarrow {\frac {1}{2}}X(\omega )+{\frac {1}{4}}\left[X(\omega +2\omega _{c})+X(\omega -2\omega _{c})\right]  f + ày+àn.... + Llam logx/x n... [*R, 0 –R [A] logx/x....+ â [grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx + rot, + transl. + acel 
/t /c/t
 .
Postado por às

Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)