geometria Graceli para ondas modulares

ondas modulares Graceli visa a amplitude de variações de formas, Ângulos, e variações em relação a sistema quadrimensional Graceli, infinitésimos sequenciais, e em relação de variações em relação ao tempo e movimentos, espaços, variações sequenciais matemáticas e ao tempo..

A forma padrão de uma onda modulada em amplitude (AM) é definida como:

$s(t)=A_{c}[1+k_{a}m(t)]cos(2\pi f_{c}t)$ + = f + ày+àn.... + Llam logx/x n... [*R, 0 –R [A] logx/x....+ â [grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx + rot, + transl. + acel /t /c/t.

$e(t)=(E_{c}+e_{m}(t))\cos(2\pi f_{c}t)$ + = f + ày+àn.... + Llam logx/x n... [*R, 0 –R [A] logx/x....+ â [grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx + rot, + transl. + acel

/t /c/t

Onde:

$E_{c}=$ Amplitude da portadora (c subscrito é de carrier- portadora)

$e_{m}(t)=$ Função do sinal modulador (m subscrito de modulador)

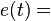$e(t)=$ Função da onda modulada

$f_{c}=$ Frequência da portadora

Como pode ser visto nesta função, a portadora é uma função cossenoidal simples com frequência fc e cuja amplitude varia de em torno de uma amplitude base Ec, de acordo com uma função de um sinal modulador em(t).

Sabe-se, que toda e qualquer função pode ser descrita como uma soma (finita ou infinita) de senoides e cossenoides. Desta forma, a função da onda moduladora pode ser descrita como uma soma de cossenoides. Vamos analisar aqui o que acontecerá se $e_{m}(t)$ for uma função cosseno simples com frequência do modulador fm:

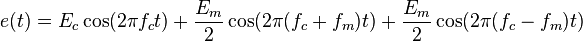$e(t)=E_{c}\cos(2\pi f_{c}t)+{\frac {E_{m}}{2}}\cos(2\pi (f_{c}+f_{m})t)+{\frac {E_{m}}{2}}\cos(2\pi (f_{c}-f_{m})t)$ + = f + ày+àn.... + Llam logx/x n... [*R, 0 –R [A] logx/x....+ â [grau] [logx/x n....+ - cx ou cv], [A] cc, + logx/xn.... osc ângulo cv, ou cx + rot, + transl. + acel

/t /c/t

geometria Graceli para ondas modulares

quarta-feira, 26 de fevereiro de 2014

Nenhum comentário:

Postar um comentário